図形の問題の解き方　加えて切る

算数を得意にする中学受験個別指導教室｜港区田町｜算数・数学専門高橋塾
こんにちは、高橋塾の高橋です。
　

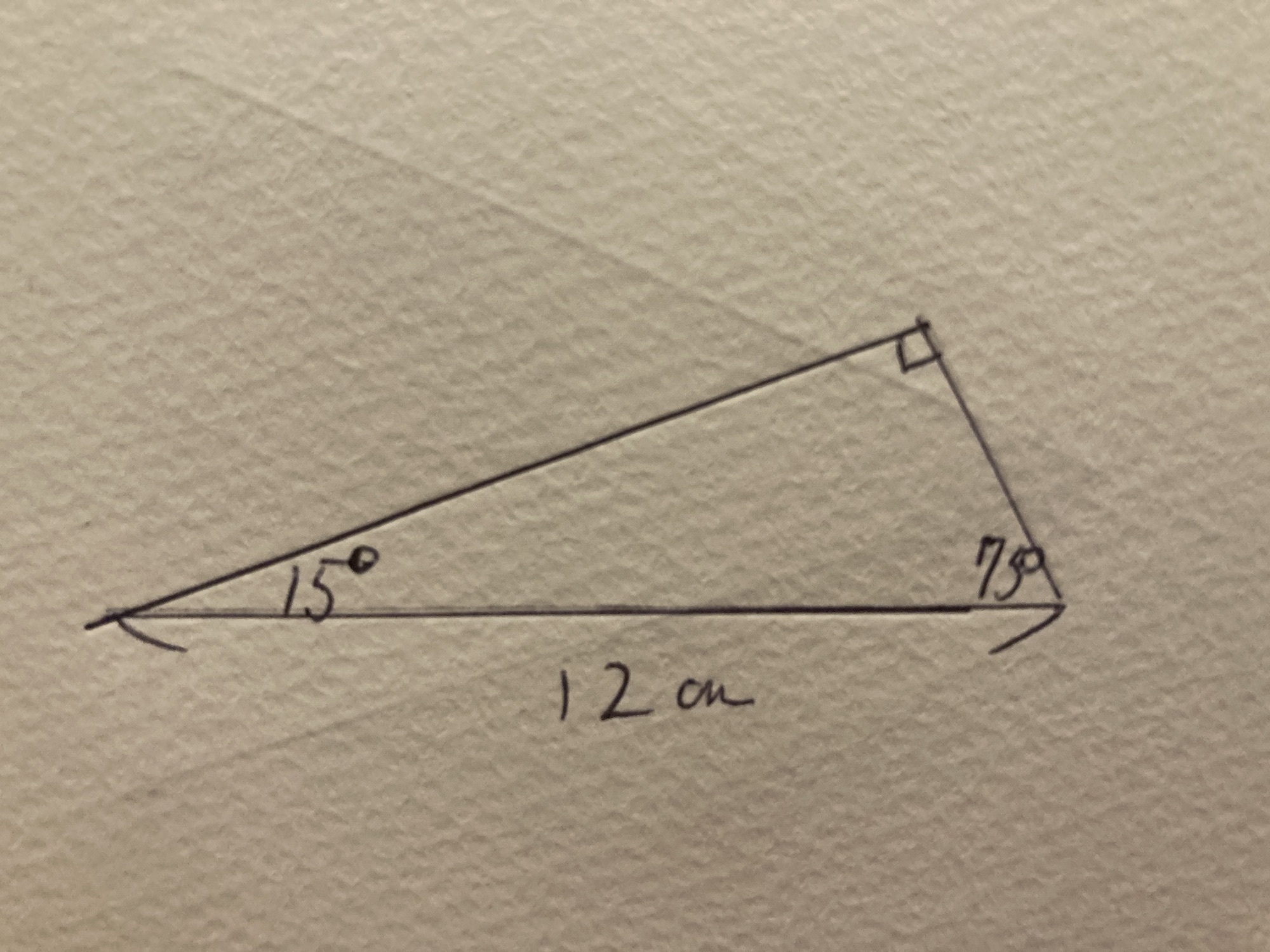
今日はこの図形の面積を求める問題を説明したいと思います。

前回説明した図形の問題と同様に加えて切っていきたいと思います。

まずこの図形はそのまま求めるのは難しいので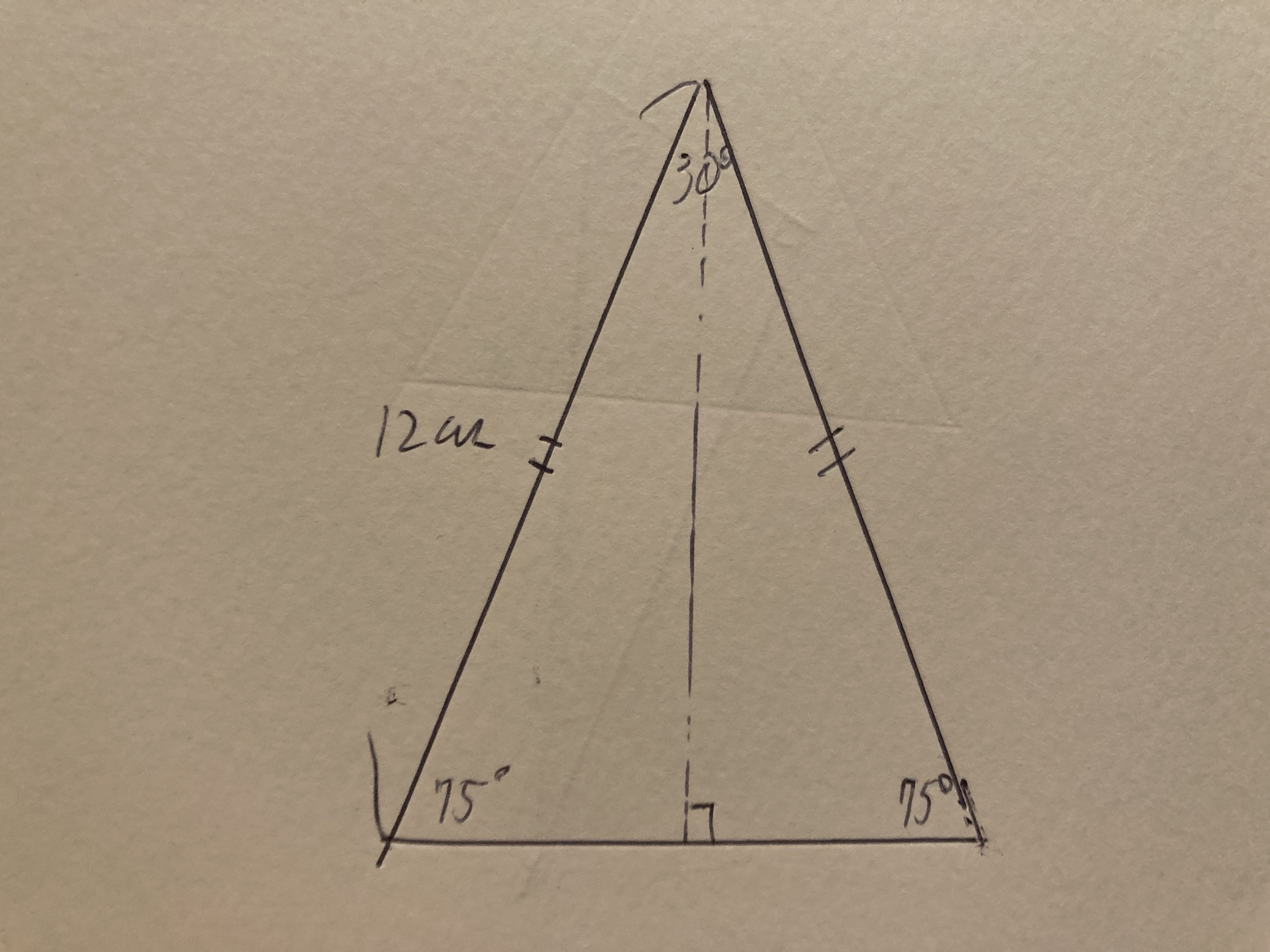


このように同じ形の図形をもう一つ加えて考えます。

そうすると30°、75°、75°の二等辺三角形になります。

ここで30°が出てきたので30°、60°、90°の直角三角形の
性質について触れたいと思います。

30°、60°、90°の直角三角形は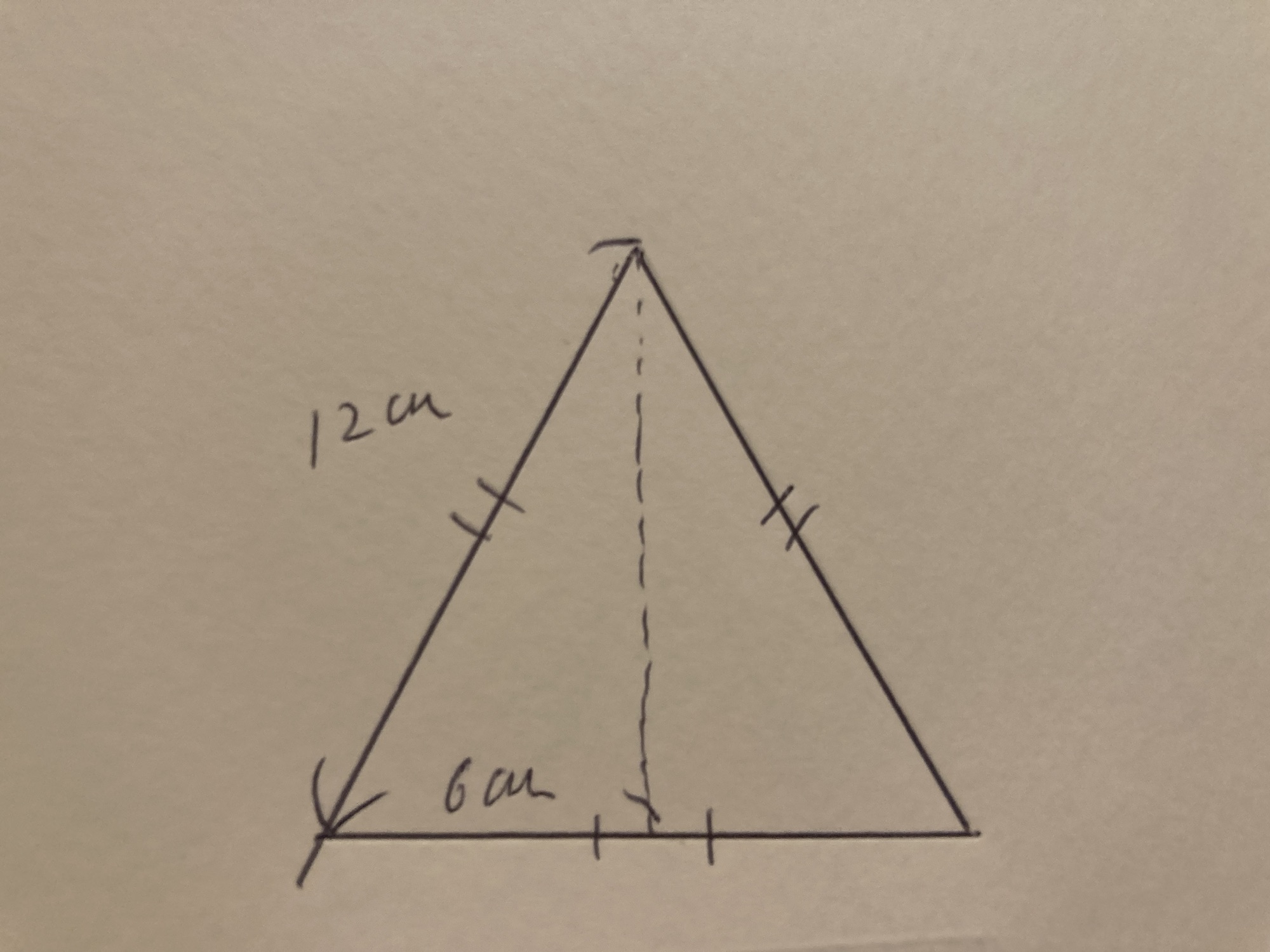



このように正三角形を半分に切った形です。

一辺が12cmの正三角形の場合底辺は半分の6cmに分かれます。

なので30°、60°、90°の直角三角形の短辺は斜辺の半分の長さになります。

この性質を利用すると先ほどの三角形はこのように見えます。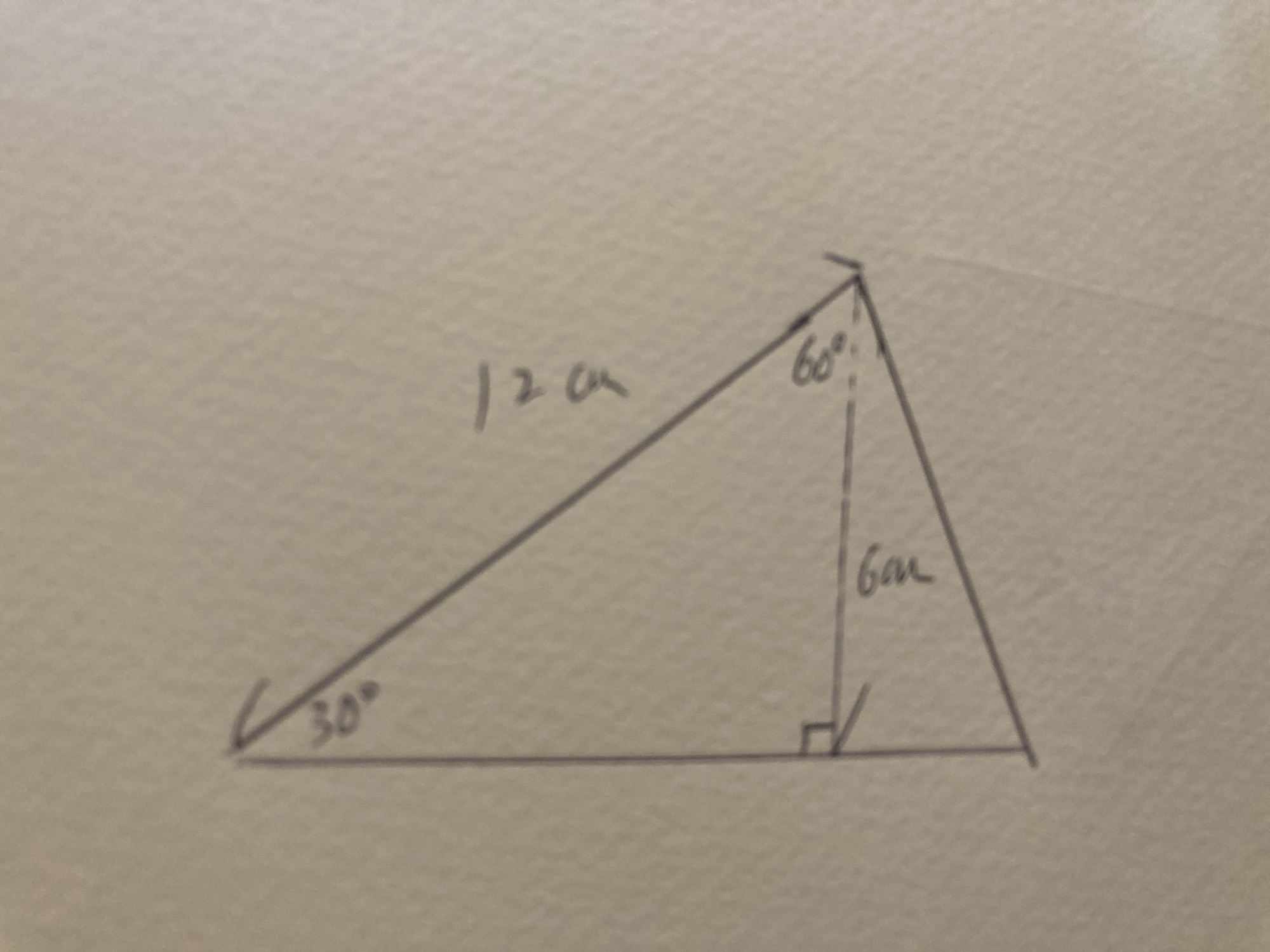



左側に30°、60°、90°の直角三角形ができるので高さは6cm。

底辺は12cmなので面積は

12×6÷2＝36㎠

これは求める三角形二つ分のため

36÷2＝18㎠

となります。

このように面積を求める問題は知っている図形に近づける

形に変えることが重要です。

ー－－－－－－－－－－－－－－－－－－－－－－－－－
生徒募集中！！
無料体験授業、ご質問など受付は下記のお問い合わせから。
お問い合わせ

Follow me!